Влияние концентраторов напряжений на эксплуатационную надежность конструкций
ООО «Региональный центр диагностики инженерных сооружений»:
ЛЮТАРЬ В.С., заведующий отделом экспертизы объектов угольной и горнорудной промышленности; ГАРКАЕВ Е.А., заведующий отделом экспертизы объектов котлонадзора и подъемных сооружений; БРАЖНИКОВ А.А., заведующий отделом экспертизы объектов химической и нефтехимической промышленности; МАРЦ Н.В., заведующий отделом экспертизы зданий и сооружений; МАТОХИН Г.В., генеральный директор, профессор, д.т.н.
Номер журнала:
Рубрика:
Очевидно, что в поле высоких (из-за концентратора) напряжений могут находиться микротрещины, размеры которых равны или меньше L:
где: l0 — максимальный размер микротрещины, не влияющий на предел выносливости металла. Так как эти микротрещины находятся в поле высоких (значительно превышающих предел выносливости) напряжений, то можно предположить, что за небольшое время эксплуатации трещины размером l0, вырастут до трещины L:
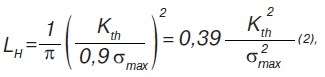
где: Lн — минимальный размер макротрещин, для которых справедливы постулаты и концепции механики разрушения.
Ввиду фактической малости указанных выше трещин последние не вызывают общего перераспределения напряжений в зоне концентратора. При этом возможны следующие два варианта:
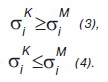
Здесь σki — интенсивность напряжений в точках зоны концентратора, размер которой равен d страгивания (см. рис. 1). В соответствии со структурной механической моделью разрушения [1] для страгивания трещины необходимо, чтобы на расстоянии d страгивания выполнялось условие Rмсе= σmax,σ0.2 = σi, где Rмсе — критерий микроскола сдеформированного материала;
σMi — интенсивность напряжений в характерных точках в области вершины трещины при отсутствии концентраторов.
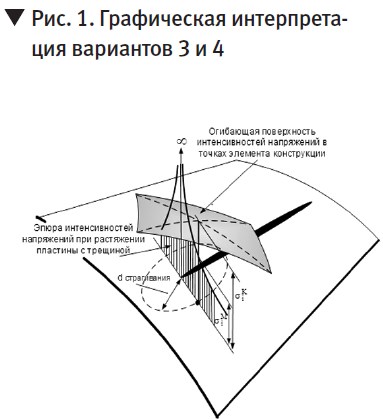
В первом случае, учитывая микроразмеры зоны предразрушения, и гипотезу о неизменности поля макронапряжений, можно считать, что характерными максимальными напряжениями будут эксплуатационные напряжения в точках зоны предразрушения (рис.1).
Во втором случае, когда причиной появления максимальных напряжений являются трещины, за характерные напряжения принимаются напряжения, вызванные присутствием трещины как концентратора.
Определим уровень напряжений в элементе конструкции, вызывающем образование и развитие трещины, при наличии в нем концентратора напряжений. Алгоритм оценки пределов выносливости будем строить на основе диаграммы деформирования с использованием степенной аппроксимации, которая приводит к зависимости [1], то есть:
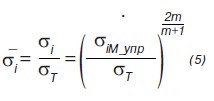
где
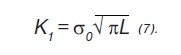
Параметр K1= σ0√πL, является коэффициентом интенсивности напряжений.
Выражение (6) с учетом зависимости (7) можно представить в виде:
Интенсивность напряжений в любой точке конструкции, определяемую по формуле
также можно представить в форме выражения:
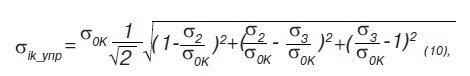
где: σ0K — номинальная (средняя) интенсивность напряжений для элемента конструкции.
Используя выражения 8 и 10 получим относительные значения интенсивностей напряжений:
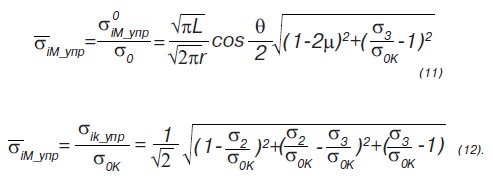
Учитывая зависимости 11 и 12, введем новый параметр, который назовем пороговым коэффициентом концентрации, равный
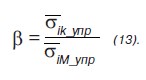
Тогда выражению (5) можно будет придать следующий вид:
где:
По определению K1th= σ0√πL. Для одноосного растяжения не возмущенной трещиной пластины следует, что σ0 = σi0, где σi0— интенсивность напряжений в точках пластины при растяжении ее усилиями интенсивности σ0. Тогда по аналогии с гипотезой единой кривой выражение для коэффициента интенсивности напряжений можно переписать в виде:
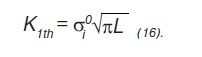
Исходя из положений структурно-механической модели [1], положим r = dстр и θ = 900. В этом случае пороговый коэффициент концентрации будет равен:
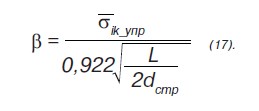
Излагаемый алгоритм справедлив при условии, что β ≥ 1.
Отношение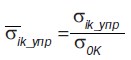 
по смыслу является коэффициентом концентрации напряжений в характерных точках зоны предразрушения, который обозначим символом αr. Однако оно не является коэффициентом концентрации напряжений в точке, где напряжение достигает максимума, то есть на величину коэффициента β сильное влияние будет оказывать градиент интенсивности напряжений в окрестности опасной точки. Тогда выражение 17 принимает вид:
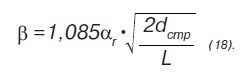
Учитывая, что при степенной аппроксимации диаграммы деформирования:
и подставляя вместо σi = Rmce• D (условие начала развития трещины L получим формулу для определения Kth0:
Таким образом, из формулы 19 следует, что произведение порогового коэффициента концентрации на пороговый коэффициент интенсивности напряжений в зоне концентрации напряжений есть величина постоянная и равная пороговому коэффициенту Kth0 для материала, то есть
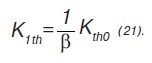
В данном случае коэффициент K1th является пороговым коэффициентом интенсивности напряжений для материала, находящегося в зоне концентратора напряжений.
В работе [1] показано, что значение Kth0 рассчитывается по сведениям о стандартных характеристиках материала. Поэтому, зная σik_упр для определенного концентратора, можно по зависимости (20) определить величину напряжений, которые вызовут развитие в концентраторе трещины.
Литература
1. Матохин Г.В. Оценка ресурса сварных конструкций из феррито-перлитных сталей.— Владивосток: Издательство ДВГТУ, 2001. — 202 с.
