Оценка безопасной эксплуатации конструкции при наличии трещиноподобных дефектов

Рассмотрим простейшую конструкцию в виде консольной балки  с прямоугольным поперечным сечением, нагруженной на конце сосредоточенной силой Р.
Согласно технической теории изгиба, описанной в любом учебнике по сопротивлению материалов,

если l,b и h — длина балки, ширина и высота прямоугольного поперечного сечения. Считается, балке ничего не угрожает при заданной нагрузке, если:

где σ_T — предел текучести материала (для хрупких материалов, наподобие камня, берется предел прочности), n — коэффициент запаса, который учитывает неточность изготовления, разброс свойств материала, последствия разрушения  и т. д.
Итак, классическая теория сопротивления материалов ограничивает сверху несущую способность балки следующим пределом:

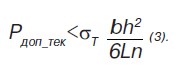
Реальная конструкция всегда содержит дефекты (как уже говорилось, дефекты самого материала и дефекты, возникшие при изготовлении и эксплуатации), и только что полученные оценки в принци­пе должны быть дополнены расчетом на безопасность от возмож­ного хрупкого разрушения. Предположим, что наиболее опасный дефект — трещина дли­ны l появилась в наиболее опас­ном месте — на поверхности бал­ки у места ее заделки в жесткую опору (рис. 1), то есть там, где растягивающие напряжения максимальны. 
При определении коэффициента интенсивности на­пряжений для краевой трещины малой глубины мы можем вос­пользоваться соответствующей формулой:

По критерию Ирвина эксплуатация конструкции будет безопасной, если:

где K1C — вязкость разрушения, а m — еще один коэф­фициент запаса. 
Оценку безопасной (с позиций линей­ной механики разрушения) эксплуатационной нагрузки мы получим, подставив выражение 4 в условие 5. Определив максимальные напряжения с помощью зависимости 1, получим

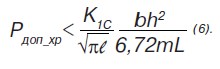
Геометрические размеры балки присут­ствуют в формулах 3 и 6 совершенно естественным образом. То же можно сказать и о прочностных ха­рактеристиках материала σ_T и K_1C. Однако в формуле 6 со­держится новый физический параметр — размер дефекта — l.
Определим отношение допускаемых нагрузок, определенных для рассмотренных случаев.

Рассмотрим тонкостен­ный цилиндрический сосуд с полусферическими доньями, заполненный газом или жидкостью под давлением р. Известно что окружные напряжения в стенках цилиндра вдвое больше продольных. Это максимальные напряжения, и разрушится наш сосуд, очевидно, лопнув вдоль осевой линии. 
Условие прочности (текучести) приводит к следующему ог­раничению безопасных рабочих давлений:

Наиболее опасными для данного сосуда будут, разумеется, поверхностные трещины, расположенные вдоль оси ци­линдра. Коэффициент интенсивности напряжений для длинной, но неглубокой трещины можно получить из формулы (4), подставив туда σ_max=pR/t:

Безопасное рабочее давление для сосуда с таким дефек­том определяется критерием Ирвина (5):

Заметим, что трещины образуются, как правило, на внутренней поверхности трубы под дейст­вием усталости или коррозии. Иногда пытаются несколько уточнить расчет, приняв во внимание непосредственное давление газа или жидкости на берегах трещины, для этого в выражение (4) нужно подставлять напряжение не как pR/t, а p(1+R/t). То есть учитывать действие давления не только на внутреннюю поверхность, но и на поверхность раскрывающейся трещины. 
Существенно ли это — зависит от величины R/t, но обычно для тонкостенных сосудов она превышает 10, и данная поправка непринципиальна. 
Для выбора того или иного дефектоскопического ме­тода существен вопрос об определении l_c — критическо­го размера дефекта, исходя из известных условий эк­сплуатации конструкции. В случае рассматриваемого цилиндрического сосуда l_c определяется из усло­вия достижения равенства в формуле (10):

Если для сосуда, находящегося под давлением, допускаемые напряжения определены по классической теории прочности, то есть σ_max= σ_T/n, то

Для обеспечения надежности конструкции важно иметь возможность с большей вероятностью обнаруживать трещины прежде, чем они достигнут критического раз­мера. Условия 11 и 12 необходимо учитывать при выработке технических требований, предъявляемых к не­разрушающему контролю. Насколько критические длины разнятся в различных материалах, можно представить, сопоставляя значения (K1C/ σT)2. Например, для типич­ной стали, используемой в сосудах давления ядерных силовых установок, эта величина составляет примерно 140 мм, а для высокопрочной авиационной стали она имеет порядок 1 мм. Приблизительно так соотносятся крити­ческие длины трещин. Следовательно, и к выбору метода контроля подход будет различный. При этом требования к точности определения размера дефекта будут определяться его местом расположения и характером напряженного состояния. Сравним критические размеры краевой и внутренней трещины (рис. 2).
Для краевой трещины:

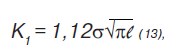
для внутренней:

Будем считать, что критическая длина трещины опре­деляется условием K₁ = K_1C, а вязкость разрушения оди­накова и в середине пластинки, и на ее краях, поэтому:

откуда:

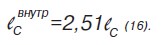
Наибольшее распространение в расчетах на прочность деталей с трещинами получил расчет по силовому критерию с использованием коэффициента интенсивности напряжений:

где  K_1C  играет ту же роль, что и истинное сопротивление разрыву S_X в расчетах деталей на прочность без трещин; K_1расч — расчетный коэффициент интенсивности напряжений около вершины трещины. Следовательно, для оценки состояния конструкции с точки зрения механики разрушения необходимо располагать значениями K_1расч и K_1С.
Таким образом, дополнительный расчет на безопасность от возможного хрупкого разрушения позволяет не только определять гарантированный безопасный уровень рабочих нагрузок, но и формировать технические требования к методам неразрушающего контроля, которые обязаны обеспечивать возможность определять размеры дефектов существенно меньше его критических значений. 

Литература
1. Броек Д. Основы механики разрушения.— М.: Высшая школа, 1980. — 368 с.