Расчет остаточного ресурса трубопроводов по характеристикам трещиностойкости

ООО «Недра»: БЫСТРОВ С.А.
директор, эксперт в области промышленной безопасности ЩЕНИН В.В., технический директор, эксперт в области промышленной безопасности МУХИН Р.С., эксперт в области промышленной безопасности
Номер журнала:
Рубрика:
Предварительно по данным механических испытаний на одноосное растяжение вычисляются параметры малоцикловой трещиностойкости:

где ΨВ — коэффициент равномерного сужения сечения при растяжении;
Ψk — коэффициент относительного сужения при разрыве;
F — исходная рабочая площадь сечения образца;
FВ — площадь сечения образца в зоне равномерного сужения;
ε0,2 = 0,002 — относительная остаточная деформация, равная 0,2 %.
Характеристики статической трещиностойкости определяются по результатам циклических испытаний образцов в соответствии с ГОСТ 25506-85:
1) разрушающее напряжение по максимальной разрушающей силе Рс для образца с трещиной:

где b — ширина образца; t — толщина образца;
2) степень снижения разрушающих напряжений от наличия трещин в образце при относительной глубине трещины, равной η = h / t = 0,5;
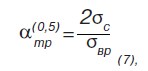
где σвр — временное сопротивление растяжению;
3) предел трещиностойкости для относительной глубины, равной η = 0,5:
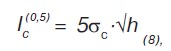
где h — полная глубина трещины на образце;
4) разрушающие кольцевые напряжения для бездефектной трубы с учетом характеристик циклической трещиностойкости:

где σ0,2 — условный предел текучести.
Допускаемая глубина трещины определяется по максимальному усредненному давлению из совместного решения двух функций, образующих равенство
Kl=lc / ml (10),
где KI — коэффициент интенсивности напряжений при максимальном усредненном давлении, МПа·√м;
Ic — предел трещиностойкости для допускаемой глубины трещины, МПа·√м;
mI — коэффициент запаса по пределу трещиностойкости, определяемый по формуле:

где σр — уровень рабочих напряжений, в данном случае равен кольцевым напряжениям при максимальном давлении:

где Dвн — внутренний диаметр трубы, м; tн — толщина стенки, м.
Коэффициент интенсивности напряжений определяется по формуле: Kl=σр√h•Y(η)(13), где Y(η) — полином, зависящий от текущего значения относительной глубины трещины η. Для образца типа 5 по ГОСТ 25506-85:
Y(η)=1,99-0,4η+18,7η2-38,48η3+53,85η4 (14).
Предел трещиностойкости определяется по формуле:

где αтр — степень разрушающих напряжений при текущем значении,

Из совместного решения уравнений (13) и (15) с учетом коэффициента m1 в соответствии с равенством (10) получается допускаемая относительная глубина трещины ηmр.
Критическая глубина трещины определяется для среднего рабочего давления за исследуемый период.
Для этого из совместного решения уравнения (13) и (15) при коэффициенте запаса по пределу трещиностойкости m1, равном единице (m1 = 1), определяется относительное значение критической глубины трещины ηкр.
Остаточный ресурс определяется по времени роста трещины от допускаемой глубины до критической при усредненном максимальном давлении перекачки по формуле:
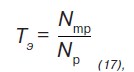 ,
,
где Np — расчетное число циклов перепада рабочего давления за один год;
Nmр — долговечность труб при циклическом нагружении (в числах циклов), определяемая по формуле:

где h0 — начальная глубина трещины, определяемая из данных диагностики. В случае отсутствия острых трещиноподобных дефектов по данным диагностики начальная глубина трещины h0 принимается равной допускаемой глубине трещины;
N0 — предельное число циклов нагружения

где коэффициент интенсивности упругопластических деформаций (20):
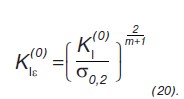
В формулах (19) и (20) с, m — параметры;
- коэффициент интенсивности напряжений, определяемый по формуле (13) для максимального усредненного рабочего давления и начальной глубины трещины.
Предельное разрешенное давление определяется по характеристикам трещиностойкости, определенным при испытаниях на малоцикловую трещиностойкость по формуле:
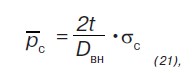
где σс — разрушающее окружное напряжение для трубы с трещиной
σθс=αmp•σθb(1-η) (22),
где η — относительная глубина трещины, вычисляемая по начальной глубине трещины, принимаемой равной допускаемой глубине;
αтр — степень снижения разрушающих напряжений;
σθb — разрушающее кольцевое напряжение для бездефектной трубы, определяемое по формуле (9).
Удмуртская Республика, г. Воткинск, ул. Луначарского, д. 32, тел.: (34145) 5-85-32, 6-46-98,
факс: (34145) 5-85-32, e-mail: nedra18@mail.ru, 58532@inbox.ru
















